Diagram Venn (Penjelasan Lengkap dan Contoh Pengunaannya)
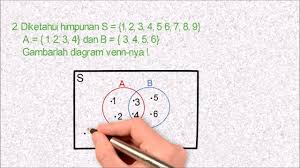

Diagram Venn adalah gambar yang digunakan untuk menyatakan hubungan antara himpunan dalam suatu kelompok objek yang memiliki kesamaan.
Biasanya, diagram Venn digunakan untuk mengambarkan himpunan yang saling berpotongan, saling lepas dan seterusnya. Jenis diagram ini digunakan untuk penyajian data secara saintifik dan teknik yang berguna dalam bidang matematika, statistika dan aplikasi komputer.
Menelusuri diagram Venn, didalamnya terdapat suatu set atau himpunan yang wajib di mengerti terlebih dahulu.
Himpunan
Himpunan adalah kumpulan objek yang dapat didefinisikan dengan jelas.
Contohnya pakaian yang kalian gunakan saat ini merupakan suatu himpunan, didalamnya termasuk topi, baju, jaket, celana dan lain sebagainya
Kalian dapat menulis suatu himpunan dengan tanda kurung, seperti berikut
{topi, baju, jaket, celana,…}
Kalian juga dapat menulis himpunan dalam suatu bilangan seperti
- Himpunan semua bilangan : {0,1,2,3…}
- Himpunan bilangan prima: {2,3,5,7,11,13,…}
Baca Juga :
Penyajian Data Kelompok Bentuk Poligon
Penyajian Data Kelompok: Histogram, Poligon, dan Ogive
Simpel bukan?
Diagram Venn yang didalamnya mengandung himpunan tadi digambarkan dalam bentuk diagram sehingga mudah dipahami. Cara mengambar diagram seperti ditunjukkan gambar dibawah.

Cara menggambar diagram Venn
- Himpunan semesta dalam diagram Venn digambarkan sebagai bentuk persegi panjang.
- Setiap himpunan yang sedang dijelaskan digambarkan berupa lingkaran atau kurva tertutup.
- Setiap anggota himpunan masing-masing digambarkan dalam noktah atau titik.
Diagram venn memiliki beberapa bentuk, untuk lebih jelasnya simak penjelasan berikut,
Bentuk Diagram Venn

Kiri ke kanan : himpunan bagian, himpunan yang sama, himpunan saling berpotongan dan himpunan saling lepas
1. Himpunan saling berpotongan
Diagram venn ini digambarkan dimana dua himpunan yang saling berpotongan karena mempunyai kesamaan. Contohnya jika terdapat himpunan A dan B, keduanya saling berpotongan apabila mempunyai kesamaan maka hal ini berarti anggota yang masuk ke dalam himpunan A termasuk juga ke dalam himpunan B.
Himpunan A berpotongan dengan himpunan B dapat ditulis A∩B.
2. Himpunan saling lepas
Himpunan A dan B bisa dikatakan saling lepas jika anggota himpunan A tidak ada yang sama dengan anggota himpunan B. himpunan yang saling lepas ini dapat ditulis A//B.
3. Himpunan Bagian
Himpunan A dapat dikatakan bagian dari himpunan B apabila semua anggota himpunan A merupakan anggota dari himpunan B.
4. Himpunan yang sama
Diagram venn ini menyatakan bahwa jika himpunan A dan B terdiri dari anggota himpunan yang sama, maka dapat kita simpulkan bahwa setiap anggota B merupakan anggota A. contoh A = {2,3,4} dan B= {4,3,2} merupakan himpunan yang sama maka kita dapat menulisnya A=B.
5. Himpunan yang ekuivalen
Himpunan A dan B dikatakan ekuivalen apabila banyaknya anggota dari kedua himpunan sama. Himpunan A ekuivalen dengan himpunan B dapat ditulis n(A)= n(B).
Dalam diagram venn terdapat empat hubungan antarhimpunan meliputi irisan, gabungan, komplemen himpunan dan selisih himpunan.
- Irisan
Irisan himpunan A dan B (A∩B) adalah himpunan yang anggota-anggotanya ada didalam himpunan A dan himpunan B.

Sebagai contoh himpunan A ={ 0,1,2,3,4,5} dan himpunan B ={3,4,5,6,7}. perhatikanlah bahwa pada kedua himpunan tersebut terdapat dua anggota yang sama yaitu 3,4 dan 5. Nah, dari kesamaan inilah bisa dikatakan bahwa irisan himpunan A dan B atau di tulis sebagai (A∩B) = {3,4,5}.
- Gabungan
Gabungan himpunan A dan B (ditulis A ∪ B) adalah himpunan yang anggota-anggotanya merupakan himpunan A atau anggota himpunan B atau anggota kedua-duanya. Gabungan himpunan A dan B dinotasikan dengan A ∪ B = {x | x ∈ A atau x ∈ B}

Sebagai contoh himpunan A = {1,3,5,7,9,11} dan B= {2,3,5,7,11,13}. Jika himpunan A dan himpunan B digabungkan maka akan terbentuk himpunan baru yang anggotanya dapat di tulis A ∪ B ={1,2,3,5,7,9,11,13}.
- Komplemen
Komplemen himpunan A (ditulis Ac) adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.

Sebagai contoh S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}. Dapat kita perhatikan bahwa semua anggota S yang bukan dari anggota A membentuk himpunan baru yaitu {0,2,4,6,8}. Maka komplemen dari himpunan A adalah Ac = {0,2,4,6,8}.
Demikian materi tentang diagram venn, semogaa kalian memahaminya dengan baik.
Artikel Terkait
- Introductions (Perkenalan)
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?