Operasi Hitung Bilangan, Urutan dan Campuran

Operasi hitung bilangan pada dasarnya dibedakan menjadi 4 jenis operasi hitung dasar. Keempat operasi hitung dasar bilangan tersebut disebut operasi aritmatika. Terdapat juga 3 operasi hitung lain yang sering digunakan yaitu perpangkatan, akar, dan tanda kurung.

Nahh pada pembahasan kali ini,otakers perlu memahami dulu apa itu definisi dari bilangan. Bilangan adalah suatu konsep dalam matematika yang digunakan untuk melakukan pencacahan dan pengukuran. Secara sederhana dapat disebutkan bahwa bilangan digunakan untuk menyatakan banyak atau jumlah suatu objek. Bilangan dilambangkan dengan angka. Salah satu bentuk bilangan yaitu bilangan bulat yang akan kita ulas pada pembahasan berikut.

1. Operasi Hitung Bilangan Bulat

Beberapa operasi hitung sederhana dalam bilangan bulat antara lain penjumlahan, pengurangan, perkalian, dan pembagian. Dalam operasi bilangan bulat penjumlahan dan pengurangan bilangan bulat dapat disajikan dalam garis bilangan sebagai berikut.

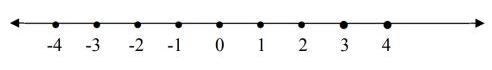
Dalam garis bilangan tersebut, terdapat bilangan bulat yang dikelompokkan bilangan bulat positif, bilangan nol dan bilangan bulat negatif.

1.Operasi Penjumlahan

Operasi penjumlahan merupakan operasi yang melibatkan tanda “ + “. Dalam garis bilangan, suatu bilangan yang dijumlahkan dengan suatu bilangan positif akan bergerak ke kanan (semakin besar). Berikut akan dijelaskan sifat-sifat dalam operasi penjumlahan.

a.Sifat Komutatif

Sifat komutatif dapat disebut sebagai sifat pertukaran. Secara umum sifat komutatif yaitu

a + b = b + a

Contoh:

3 + 9 = 9 + 3 = 12

b. Sifat Asosiatif

Sifat asosiatif ini bisa disebut juga dengan sifat pengelompokan. Secara umum sifat asosiatif dituliskan dengan

(a + b) + c = a + (b + c)

Contoh:

(5 + 6) + 2 = 5 + (6 + 2) = 13

c. Sifat identitas terhadap penjumlahan

Unsur identitas terhadap operasi penjumlahan adalah bilangan 0. Mengapa 0 dikatakan sebagai unsur identitas terhadap penjumlahan? Karena jika kita menjumlahkan suatu bilangan dengan 0, hasil operasi penjumlahan akan tetap bilangan itu sendiri. Secara umum dituliskan dengan

0 + a = a + 0

Contoh:

5 + 0 = 0 + 5 = 5

d. Unsur invers terhadap penjumlahan

Invers (lawan) dari a adalah –a.

Invers (lawan) dari –a adalah a.

Secara umum sifat invers ini dituliskan dengan

a + (-a) = 0

Contoh :

6 + (-6) = 0

e. Sifat tertutup

Penjumlahan berlaku sifat tertutup artinya penjumlahan bilangan bulat akan menghasilkan bilangan bulat juga.

Jika a dan b adalah bilangan bulat maka a + b = c dengan c merupakan bilangan bulat.

Contoh:

4 + 5 = 10  

4, 5, dan 10 merupakan bilangan bulat.

2. Operasi Pengurangan

Operasi pengurangan merupakan operasi yang melibatkan tanda “ – “. Dalam garis bilangan, suatu bilangan yang dikurangi dengan suatu bilangan positif akan bergerak ke kiri (semakin kecil).

Berikut akan dijelaskan sifat-sifat dalam operasi pengurangan. Untuk suatu bilangan bulat berlaku:

a – b = a + (-b)

a – (-b) = a + b

 

Baca Juga:

Sifat-Sifat Operasi Hitung Matematika

Operasi Hitung Campuran Bilangan Bulat

Operasi Hitung Matematika Beserta Soal dan Pembahasan

 

contoh:

3 – 1 = 3 + (-1) = 2

1. – (-2) = 4 + 2 = 6

a.Tidak berlaku sifat komutatif dan assosiatif

a – b ≠ b – a

(a – b) – c ≠ a – (b – c)

Contoh:

4 – 2 ≠ 2 – 4

(6 – 2) – 1 ≠ 6 – (2 – 1)

b. Pengurangan yang melibatkan bilangan 0

a – 0 = a  dan 0 – a = -a

Contoh:

4 – 0 = 4 dan 0 – 4 = -4

c. Bersifat tertutup

Pengurangan yang melibatkan dua bilangan bulat, hasil operasinya juga merupakan bilangan bulat.

Jika a dan b merupakan bilangan bulat, maka a – b = c dengan c merupakan bilangan bulat.

Contoh:

7– 2 = 5.  

7, 2 dan 5 merupakan bilangan bulat.

3. Operasi Perkalian

Operasi perkalian merupakan operasi matematika yang melibatkan tanda “×”. Perkalian dapat disebut sebagai penjumlahan yang berulang.

Sifat-sifat operasi perkalian dijelaskan pada bagian berikut.

a.Hasil perkalian dua bilangan bulat positif merupakan bilangan bulat positif.

(+a) x (+b) = (+) ab

(+ a) x (- b) = (-) ab

(- a) x (+ b) = (-) ab

(- a) x (- b) = (+) ab

b. Sifat komutatif

a x b = b x a

Contoh:  

9 x 2 = 2 x 9 = 18

c. Sifat assosiatif

(a x b) x c = a x (b x c)

Contoh:

(3 x 2) x 4 = 3 x (2 x 4) = 24

d. sifat distributif.

a x (b + c) = ab + ac

Contoh:

3 x ( 4 + 2) = (3 x 4) + (3 x 2) = 12 + 6 = 18

e. Unsur identitas

Unsur identitas terhadap perkalian adalah 1. Perkalian suatu bilangan dengan bilangan 1 akan menghasilkan bilangan itu sendiri.

a x 1 = a

Contoh:

21 x 1 = 21.

f. Bersifat tertutup

Perkalian dua bilangan bulat menghasilkan bilangan bulat pula.

Jika a dan b bilangan bulat, maka a x b = c dengan c merupakan bilangan bulat.

Contoh:

 7 x 2 = 14.     

7, 2, 14 merupakan bilangan bulat.

4. Operasi Pembagian

a.Hasil bagi

(+a) : (+b) = (+) ab

(+a) : (-b) = (-) ab

(-a) : (-b) = (+) ab

b. Hasil bagi bilangan bulat dengan 0 (nol) tidak terdefinisi.

a : 0 = (tidak terdefinisi)

Contoh:

5 : 0 = (tidak terdefinisi)

c. Tidak berlaku sifat komutatif dan assosiatif.

a : b ≠ b : a

(a : b) : c ≠ a : (b : c)

Contoh:

6 : 2 ≠ 2 : 6

6: 3) : 2 ≠ 6 : (3 : 2)

5. Tanda Kurung

Operasi matematika yang menggunakan tanda kurung harus dikerjakan terlebih dahulu atau diprioritaskan. Berikut jenis tanda kurung yang sering digunakan dalam ilmu matematika.

a. Tanda kurung () yang disebut bracket untuk operasi bilangan secara umum.

b. Tanda kurung siku [] yang disebut square bracket, yang biasa digunakan dalam operasi vektor, matriks, dan interval.

c. Tanda kurung kurawal {} yang disebut curly bracket, yang biasa digunakan dalam notasi himpunan.

Contoh :

(5 + 6) x 3 =

11 x 3 = 33

6.Perpangkatan

Perpangkatan adalah operasi hitung perkalian berulang dengan bilangan yang dipangkatkan sebanyak pangkatnya.

Adapun sifat-sifat umum operasi perpangkatan

1) a^m x aⁿ = a^m+n

2) a^m : aⁿ = a^{m-n ,} untuk m>n dan b ≠ 0

3) (a^m)ⁿ = a^mn

4) (ab)^m = a^m b^m

5) (a/b)^m = a^m/b^m , untuk b ≠ 0

7.Operasi Akar

Operasi akar adalah kebalikan dari operasi perpangkatan atau dalam ilmu matematika disebut invers dari perpangkatan.

B. Urutan Operasi Hitung

Saat menyelesaikan perhitungan yang menggunakan banyak operasi hitung sekaligus, kita perlu mengetahui urutan operasi hitung yang didahulukan. Secara umum berikut urutan operasi hitung dasar matematika (urutan pertama adalah paling diprioritaskan)

1)Tanda Kurung

2) Perpangkatan dan Akar Bilangan

3) Perkalian dan Pembagian

4) Penjumlahan dan Pengurangan

C. Operasi Hitung campuran

Operasi hitung campuran merupakan gabungan dari dua atau lebih operasi hitung biasa. Untuk menyelesaikan operasi hitung campuran, harus berpatokan pada urutan operasi hitung yang telah dijelaskan di atas.

Contoh 1:

25 – 3 x 8 =

Pada soal diatas terdapat dua operasi hitung bilangan yaitu pengurangan dan perkalian. Karena sesuai urutan pengerjaan operasi hitung, maka operasi perkalian perlu dikerjakan terlebih dahulu.

25 – 3 x 8 =

25 – 24 = 1

Contoh 2 :

(7 – 4) x (1 + 2) =

Karena dalam urutan oprasi hitung bilangan soal yang di dalam kurung haruslah dikerjakan terlebih dahulu. Maka didapatkan

(7 – 4) x (1 + 2) =

     3     x     3     =

            9

Itulah tadi penjelasan mengenai operasi bilangan bulat, urutan dan bagaimana pula cara mengerjakan operasi bilangan campuran. Semoga kalian dapat memahaminya dengan baik ya