Irisan Kerucut Beserta Soal dan Pembahasan

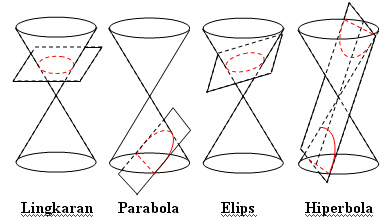
Irisan Kerucut dalam matematika merupakan lokus dari semua titik yang membentuk kurva dua dimensi, dimana kurva tersebut terbentuk dari irisan sebuah kerucut dengan sebuah bidang. Terdapat 4 macam irisan kerucut, yaitu lingkaran, parabola, elips serta hiperbola.

 

DEFINISI

Lingkaran

Lingkaran merupakan tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu.

• Titik tertentu itu disebut pusat lingkaran
• Jarak yang sama itu disebut jari-jari/radius (r)

Luas lingkaran = π.r² (r = jari-jari)

Contoh gambar:

Lingkaran dengan pusat (0, 0) dan jari-jari 2

Parabola

Parabola merupakan tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik dan sebuah garis tertentu.

• Titik itu disebut fokus/titik api (F)
• Garis tertentu itu disebut garis direktris/garis arah
• Garis yang melalui F dan tegak lurus dengan garis arah disebut sumbu simetri parabola
• Titik potong parabola dengan sumbu simetri disebut puncak parabola
• Tali busur terpendek yang melalui F disebut Latus Rectum → tegak lurus dengan sumbu simetri

Contoh gambar:

Parabola horisontal dengan puncak (0,0), fokus (1, 0), dan garis arah x = –1

Parabola vertikal dengan puncak (0,0), fokus (0, 1), dan garis arah y = –1

 

Elips

(1) Elips merupakan tempat kedudukan titik-titik yang jumlah jaraknya terhadap 2 titik tertentu tetap.

• Jumlah jarak itu = 2a (untuk elips horisontal) atau 2b (untuk elips vertikal)
• Kedua titik tetap itu disebut fokus (F) → jarak antara F₁ dan F₂ adalah 2c

(2) Elips merupakan tempat kedudukan semua titik yang perbandingan jaraknya terhadap sebuah titik dan sebuah garis tetap = e (eksentrisitet), dimana 0 < e < 1

• Titik itu adalah fokus (F), dan garis itu adalah garis arah.
• Ruas garis yang melalui kedua fokus dan memotong elips disebut sumbu mayor
• Pusat elips adalah titik tengah F₁ dan F₂
• Ruas garis yang melalui pusat, tegak lurus sumbu mayor dan memotong elips disebut sumbu minor

Luas Elips = π.a.b  (a = ½ panjang horisontal; b = ½ panjang vertikal)

Contoh gambar:

Elips horisontal dengan pusat (0, 0), puncak-puncak (5, 0), (–5, 0), (0, 4), (0, –4), fokus (3, 0), (–3, 0), dan garis arah x = ±25/3

Elips vertikal dengan pusat (0, 0), puncak-puncak (√2, 0), (–√2, 0), (0, 2), (0, –2), fokus (0,√2), (0, –√2), dan garis arah y = ±2√2/3

Hiperbola

(1) Hiperbola merupakan tempat kedudukan titik-titik yang selisih jaraknya terhadap 2 titik tertentu tetap

• Selisih jarak itu = 2a (untuk elips horisontal) atau 2b (untuk elips vertikal)
• Kedua titik tetap itu disebut fokus (F) → jarak antara F₁ dan F₂ adalah 2c

(2) Hiperbola merupakan tempat kedudukan semua titik yang perbandingan jaraknya terhadap sebuah titik dan sebuah garis tetap = e , dimana e > 1

• Titik-titik tertentu itu disebut fokus (F₁ dan F₂)
• Garis yang melalui titik-titik F₁ dan F₂ disebut sumbu transvers (sumbu utama)/ sumbu nyata
• Titik tengah F₁ dan F₂ disebut pusat hiperbola (P)
• Garis yang melalui P dan tegak lurus sumbu transvers disebut sumbu konjugasi (sumbu sekawan)/ sumbu imajiner
• Titik-titik potong hiperbola dan sumbu transvers disebut puncak hiperbola
• Garis yang melalui fokus dan tegak lurus pada sumbu nyata dan memotong hiperbola di 2 titik → ruas garis penghubung kedua titik tersebut = Latus Rectum

Contoh gambar:

Hiperbola horisontal dengan pusat (0, 0), puncak (2, 0), (–2, 0), fokus (√6, 0), (–√6, 0),  dan asimtot y = ± ½√2 x

Hiperbola vertikal dengan pusat (0, 0), puncak (√2, 0), (–√2, 0), fokus (0, √6), (0, –√6),  dan asimtot y = ± ½√2 x

PERSAMAAN

Perhatikan beberapa Tips berikut ini :

Cara membedakan persamaan-persamaan irisan kerucut:

• Pada persamaan Lingkaran: koefisien x² dan y² sama
• Pada persamaan Parabola: hanya salah satu yang bentuknya kuadrat (x² saja atau y² saja)
• Pada persamaan Elips: koefisien x² dan y² bertanda sama (sama-sama positif atau sama-sama negatif)
• Pada persamaan Hiperbola: koefisien x² dan y² berbeda tanda (salah satu positif, yang lain negatif)

Contoh:

• 3x² + 3y² + 6x + y = 5 → Persamaan Lingkaran
• 3x² + 3y + 6x = 5 → Persamaan Parabola
• 3x² + y² + 6x + y = 5 → Persamaan Elips
• 3x² – 3y² + 6x + y = 5 → Persamaan Hiperbola

 

KEDUDUKAN TITIK TERHADAP IRISAN KERUCUT

Dalam mencari kedudukan titik terhadap irisan kerucut dapat menggunakan cara sebagai berikut :

1. Jadikan ruas kanan pada persamaan irisan kerucut = 0
2. Masukkan koordinat titik pada persamaan:

→    Jika hasil ruas kiri < 0 → titik berada di dalam irisan kerucut

→    Jika hasil ruas kiri = 0 → titik berada tepat pada irisan kerucut tersebut

→    Jika hasil ruas kanan > 0 → titik berada di luar irisan kerucut

Contoh:

Tentukanlah kedudukan titik (5, –1) terhadap elips dengan persamaan 3x² + y² + 6x + y = 5?

Penyelesaian :

3x² + y² + 6x + y – 5 = 0

Ruas kiri: 3.5² + (–1)² + 6.5 + (–1) – 5  = 75 + 1 + 30 – 1 – 5 =100

→ 100 > 0, jadi titik (5, –1) berada di luar elips tersebut

 

KEDUDUKAN GARIS TERHADAP IRISAN KERUCUT

Dalam mencari kedudukan garis terhadap irisan kerucut dapat digunakan cara berikut ini.

1. Persamaan garis dijadikan persamaan x = … atau y = …
2. Substitusikan persamaan garis itu pada persamaan irisan kerucut, sehingga menghasilkan suatu persamaan kuadrat.
3. Hitung nilai Diskriminan (D) dari persamaan kuadrat tersebut (Ingat! D = b² – 4.a.c)

→    Jika D < 0 → garis berada di luar irisan kerucut

→    Jika D = 0 → garis menyinggung irisan kerucut di 1 titik

→    Jika D > 0 → garis memotong irisan kerucut di 2 titik

Contoh:

Tentukanlah  kedudukan garis x + 2y = 4 terhadap parabola dengan persamaan 3x² + 3y + 6x = 5

Penyelesaian :

Garis: x = 4 – 2y

3(4 – 2y)² + 3y + 6(4 – 2y) – 5 = 0

3(16 – 16y + 4y²) + 3y + 24 – 12y – 5 = 0

48 – 48y + 12y² + 3y + 24 – 12y – 5 = 0

12y² – 57y + 67 = 0

D = b² – 4.a.c = (–57)² – 4.12.67 = 33

Karena D > 0 maka garis x + 2y = 4 memotong parabola tersebut

 

PERSAMAAN GARIS SINGGUNG

dalam hal ini m merupakan gradien.

Persamaan garis singgung pada titik (x₁, y₁)

Dalam menyelesaikan persamaan garis singgung ini selalu gunakanlah  sistem bagi adil, dimana

(…)² menjadi (…).(…)

(…) menjadi ½ (…) + ½ (…)

Pada salah satu (…) titik ke persamaan hasil bagi adil akan dimasukkan koordinat titik yang diketahui

1. Jika titik terletak pada irisan kerucut, akan menghasilkan persamaan garis singgung
2. Jika titik terletak di luar irisan kerucut, akan menghasilkan persamaan garis polar

Kemudian potongkan garis polar dengan irisan kerucut untuk mendapatkan 2 titik potong

Selanjutnya masukkan kedua titik potong itu ke dalam persamaan hasil bagi adil untuk mendapatkan 2 buah persamaan garis singgung

Untuk lebih jelasnya perhatikan beberapa contoh berikut :

Contoh 1:

Tentukanlah persamaan garis singgung pada lingkaran x² + y² + 4x = 13 pada titik (2, 1)?

Jawab :

(2, 1) terletak pada lingkaran (2² + 1² + 4.2 = 13)

Persamaan bagi adil:

x₁.x + y₁.y + 2.x₁ + 2.x = 9

Masukkan (2, 1) sebagai x₁ dan y₁:

2.x + 1.y + 2.2 + 2.x = 9

4x + y – 5 = 0 → persamaan garis singgung

 

Contoh 2:

Tentukanlah persamaan garis singgung pada lingkaran x² + y² + 4x = 13 pada titik (4, 1)?

Jawab :

(4, 1) terletak di luar lingkaran (4² + 1² + 4.4 = 33 > 16)

Persamaan bagi adil:

x₁.x + y₁.y + 2.x₁ + 2.x = 9

Masukkan (4, 1) sebagai x₁ dan y₁:

4.x + 1.y + 2.4 + 2.x = 9

6x + y – 1 = 0 → persamaan garis polar

y = 1 – 6x

Substitusikan persamaan garis polar ke dalam persamaan lingkaran:

x² + (1 – 6x)² + 4x – 13 = 0

x² + 1 – 12x + 36x² + 4x – 13 = 0

37x² – 8x – 12 = 0

Selanjutnya gunakan rumus abc untuk mencari akar-akarnya:

Masukkan (x₁, y₁) dan (x₂, y₂) ke dalam persamaan hasil bagi adil

Materi Irisan Kerucut ini semoga dapat bermanfaat untuk sobat semua,