Bilangan Berpangkat Lengkap Soal dan Pembahasan

Pengertian Bilangan Berpangkat

Bilangan berpangkat adalah bilangan yang berfungsi untuk menyederhanakan  penulisan dan penyebutan suatu bilangan yang memiliki faktor-faktor perkalian yang sama. 

Contoh: 2x2x2x2x2x2 =… atau 5x5x5x5x5x5 =…

Perkalian bilangan-bilangan dengan faktor-faktor yang sama seperti ini biasa disebut sebagai perkalian berulang. Bayangkan jika yang dikalikan angkanya sangat banyak, maka kita pun juga akan sangat ribet dalam menulisnya karena sangking banyaknya untuk satu kali bilangan perkalian tersebut. Setiap perkalian berulang dapat dituliskan secara ringkas dengan menggunakan notasi angka bilangan berpangkat.  Contoh:

2x2x2x2x2 ini dapat kita ringkas menggunakan bilangan berpangkat menjadi 2⁵

5x5x5 dapat diringkas dengan bilangan berpangkat menjadi 5³

Cara membacanya: 2⁵    : Dua pangkat 5

Pangkat diatas berfungsi untuk menentukan jumlah faktor yang di ulang.

Rumus bilangan berpangkat adalah  “aⁿ=a×a×a×a…sebanyak n kali“.

Baca Juga : 

Soal Bilangan Berpangkat Bulat Positif, Negatif dan Nol

Contoh Soal Bilangan Berpangkat dan Pembahasannya

Contoh Soal Bilangan Berpangkat beserta Jawaban

Jenis – Jenis Bilangan Berpangkat

Ada beberapa jenis bilangan berpangkat yang paling sering dibahas, yaitu: bilangan berpangkat positif (+), bilangan berpangkat negatif (-) dan bilangan berpangkat nol (0).

1. Bilangan Berpangkat Positif

Bilangan berpangkat positif adalah bilangan yang memiliki pangkat atau eksponen positif. Apa itu eksponen? eksponen ialah penyebutan lain dari pangkat. Bilangan berpangkat positif memiliki sifat-sifat tertentu, yang mana bilangan tersebut terdiri dari a, b, sebagai bilangan real dan m, n, yang merupakan bilangan bulat positif. Ada beberapa sifat-sifat bilangan berpangkat positif yaitu sebagai berikut:

1. a^m x aⁿ = a^m+n
2. a^m : aⁿ = a^{m-n ,} untuk m>n dan b ≠ 0
3. (a^m)ⁿ = a^mn
4. (ab)^m = a^m b^m
5. (a/b)^m = a^m/b^m , untuk b ≠ 0

Contoh :

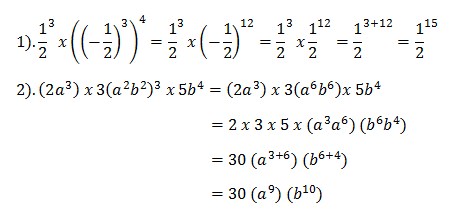
2. Bilangan Berpangkat Negatif

Selanjutnya adalah pengertian bilangan berpangkat negatif yaitu bilangan yang memiliki pangkat atau eksponen negatif (-). Adapun sifat-sifat bilangan berpangkat negatif yaitu:

Apabila a∈R, a ≠ 0, dan n ialah bilangan bulat negatif, jadi:

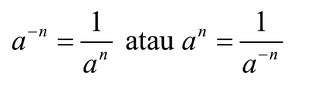
Contoh :

 Tentukan dan nyatakan dengan pangkat positif bilangan berpangkat berikut ini:

3. Bilangan Berpangkat Nol

selain bilangan berpangkat positif dan bilangan berpangakt negatif diatas, ternyata dalam ilmu matematika juga ada bilangan berpangkat nol (a). Untuk itu yuk mari kita pelajari lebih dalam.

Sebelumnya kita telah mengetahui bahwa sifat-sifat bilangan berpangkat, yaitu:

  . Berdasarkan sifat pembagian bilangan berpangkat positif dapat tersebut maka kita peroleh: .

Sehingga sifat untuk bilangan berpangkat nol (0) ialah “Apabila a adalah bilangan riil dan a tidak sama dengan 0, maka "

Contoh :

1. 8² x a⁰ = 64 x 1 = 64

2. 5² x (a + b)²(a - b)⁰​​​​​ = 5² x (a + b)² x 1 = 25 x (a² + 2ab + b²)

Baca Juga :

Bilangan Berpangkat : Sifat-Sifat dan Contoh Soal

Bilangan Berpangkat 2 Lengkap dengan Contoh Soal dan Pembahasan

Bilangan Berpangkat n Lengkap dengan Contoh Soal dan Pembahasan

Untuk lebih jelasnya, kalian bisa menyimak video materi Bilangan Berpangkat yang ada di bawah ini ya