Contoh Soal dan Pembahasan Pendapatan Maksimum atau Minimum

Contoh soal dan pembahasan
1. Pemilik sebuah colt box mendapat pesanan untuk mengantar barang yang berbentuk kemasan I dengan berat 10kg dan Kemasan II dengan berat 8 kg. Sebuah colt box hanya mampu menampung 300 kemasan. dengan berat maksimum 2800 kg. Jika biaya angkut untuk kemasan I Rp. 20.000,- dan kemasan II Rp. 18.000,- maka banyaknya masing-masing kemasan agar memperoleh pendapatan maksimum yaitu
Jawab :
Untuk menyelesaikan persoalan Maksimum ataupun minimum agar lebih mudah kamu bisa membuat tabel seperti berikut
| Kemasan I | Kemasan II | Maksimum | |
| Jumlah | X | Y | 300 |
| Berat | 10 kg | 8 kg | 2800 kg |
| Pendapatan Max | 20.000 x | 18.000 y | ? |
Jika diubah dalam bentuk Matematika akan didapatkan persamaan.
x + y = 300 (pers 1)
10 x + 8 y = 2800 (pers 2)
Target pendapatan Maks ? 20.000 x + 18.000 y
* Mencari nilai x,y dari perpotongan persamaan 1 & 2
x + y = 300 / x10 10 x + 10 y = 3000
10 x + 8 y = 2800 / x1 10 x + 8 y = 2800 -
2 y = 200
y = 100
Masukkan nilai y kedalam pers 1.......... x + y = 300
x + 100 = 300
x = 300 -100 = 200
Sehingga didapatkan nilai (x,y) =(200,100)
Sehingga Nilai pendapatan akan Maksimumnya dengan Kemasan I berjumlah 200 dan Kemasan II berjumlah 100
Jika yg ditanya biaya pendapatan maksimum maka masukkan nilai (x,y) kedalam persamaan maksimum 20.000 x + 18.000 y sehingga akan didapat nilai yaitu 5.800.000 .
2. Biaya produksi satu buah payung jenis A adalah Rp20.000,00 per buah, sedangkan biaya satu buah produksi payung jenis B adalah Rp30.000,00. Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sedangkan banyaknya payung jenis B yang akan diproduksi minimal adalah dari 50 buah. Jumlah maksimal produksi kedua payung tersebut adalah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah ….
A. Rp2.000.000,00
B. Rp2.300.000,00
C. Rp2.200.000,00
D. Rp2.100.000,00
E. Rp2.000.000,00
Tonton Video Mencari Nilai Maksimum dan Minimum
Memahami Sistem Persamaan Linier Dan Metode Penyelesaiannya
Pembahasan:
Pemisalan:
x = banyak payung A
y = banyak payung B
Model matematika dari permasalahan tersebut adalah:
Fungsi tujuan: meminimumkan
![Rendered by QuickLaTeX.com \[ f(x,y) = 20.000x + 30.000y \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-040307f3278b90966661b9a077bffee7_l3.png)
Fungsi kendala:
![Rendered by QuickLaTeX.com \[ x \geq 40 \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-47a1fd058d85fb040896e6f2d6499d24_l3.png)
![Rendered by QuickLaTeX.com \[ y \geq 50 \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-5c8b661645cad4187fffe66df3cb3e40_l3.png)
![Rendered by QuickLaTeX.com \[ x + y \leq 100 \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-9e26e6ec6fe2c5d6dda9830d901e844e_l3.png)
Daerah penyelesaian yang memenuhi permasalahan:
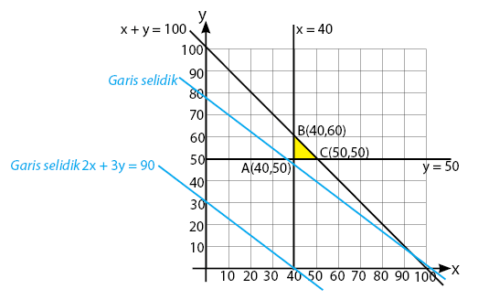
Nilai minimim akan diperoleh melalui titik koordinat yang dilalui garis selidik yang pertama kali, yaitu titik A(40, 50). Sehingga, biaya produksi minimum adalah
![Rendered by QuickLaTeX.com \[ f(40,50) = 20.000(40) + 30.000(50) \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-c179239eb749ca68e9cc306a34d76875_l3.png)
![Rendered by QuickLaTeX.com \[ f(40,50) = 800.000 + 1.500.000 \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-ae4a9781fe7e615b71314abdeaffe9f9_l3.png)
![Rendered by QuickLaTeX.com \[ f(40,50) = 2.300.000 \]](http://idschool.net/wp-content/ql-cache/quicklatex.com-dc62b6b54f3c61d830613cbb76be1762_l3.png)
Jawaban: B
3. Pemilik sebuah colt box mendapat pesanan untuk mengantar barang yg berbentuk kemasan 1 dengan berat 10kg dan kemasan 2 dengan berat 8kg.Sebuah colt box hanya mampu menampung 300 kemasan.Dengan berat maksimum 2.800kg.Jika biaya angkut untuk kemasan 1 Rp 20.000 dan kemasan 2 Rp 18.000,maka banyaknya masig masing kemasan memperoleh pendapatan maksimum,yaitu!
Pembahasan:
Dimisalkan kemasan I adalah x dan kemasan II adalah y, model matematika yang terbentuk :
(a) x + y ≤ 300.
(b) 10x + 8y ≤ 2.800 ➡ 5x + 4y = 1.400.
(c) Pendapatan yang diinginkan : f(x,y) = 20.000x + 18.000y
karena x dan y merupakan jumlah kemasan, berarti nilai x dan y adalah bilangan real, yaitu bernilai positif dan bilangan bulat : x ≥ 0 dan y ≥ 0.
Eliminasi persamaan (a) dan (b), hilangkan variabel y:
x + y = 300 |×4| 4x + 4y = 1.200
5x + 4y = 1.900 |×1| 5x + 4y = 1.400 –
-x = -200 ➡ x = 200
Substitusi nilai x ke persamaan (a):
x + y = 300
200 + y = 300
y = 300 – 200 = 100
Jadi banyaknya masing–masing kemasan agar memperoleh pendapatan maksimum, yaitu 200 kemasan I dan 100 kemasan II.
4. Seorang pedagang buah-buahan menjual jeruk dan mangga. Jeruk dan mangga di beli dari petani dengan harga Rp8.000/kg dan Rp12.000/kg dan dijual dengan mendapat keuntungan masing-masing 40% dan 30%. Modal yang ia miliki sebesar Rp 3.840.000 dan tempat untuk berjualan hanya dapat menampung maksimum 40kg buah buahan. Keuntungan maksimum yang diperoleh pedagang tersebut adalah
Pembahasan:
Diketahui jeruk = x dan mangga = y.
Seorang pedagang buah-buahan menjual jeruk dan mangga.
Tempat untuk berjualan hanya dapat menampung maksimum 40 kg buah-buahan, artinya x + y ≤ 40
Jeruk dan mangga dibeli dari petani masing-masing harganya Rp8.000 dan Rp12.000 dan modal yang dimilikinya Rp3.840.000, artinya
8.000x + 12.000y ≤ 3.840.000
⇔ 8x + 12y ≤ 3.840
⇔ 2x + 3y ≤ 960
Sehingga, diperoleh sistem pertidaksamaan
x + y ≤ 40
2x + 3y ≤ 960
x ≥ 0, y ≥ 0.
Kita ubah dahulu pertidaksamaan linear tersebut menjadi persamaan linear, diperoleh
x + y = 40 | . 2|
2x + 3y = 960 | . 1|
2x + 2y = 80
2x + 3y = 960
____________-
⇔ -y = -880
⇔ y = 880
Kemudian, y = 880 kita substitusikan ke persamaan
x + y = 40
⇔ x = 40 - y
⇔ x = 40 - 880
⇔ x = -840 (tidak mungkin)
Keuntungan maksimum menjual jeruk dan mangga masing-masing 40% dan 30%, artinya
40% = (untung jeruk/8000) . 100%
⇔ untung jeruk = 40 . 80
⇔ untung jeruk = 3.200
30% = (untung mangga/12.000) . 100%
⇔ untung mangga = 30 . 120
⇔ untung mangga = 3.600
f(x, y) = 3.200x + 3.600y
Kita substitusi titik-titik ke fungsi tersebut
f(40, 0) = 3200 . 40 + 0 = 128.000
f(0, 40) = 0 + 3600 . 40 = 144.000
f (0, 320) = 0 + 3600 . 320 = 1.152.000
f(480, 0) = 3200 . 480 + 0 = 1.536.000
f(-840, 880) = 3200 . (-840) + 3600 . 880 = -2.688.000 + 3.168.000 = 480.000
Keuntungan maksimum yang diperoleh pedagang adalah Rp1.536.000.
5. Sebuah pabrik barang elektronik mampu memproduksi x unit komputer per bulan dengan biaya setiap unitnya ( 2000 + 8000/x ) ribu rupiah.Pendapatan pabrik dari penjual x unit komputer dalam satu bulan (18.000x-80x2) ribu rupiah keuntungan maksimum diperoleh pada saat memproduksi komputer sebanyak .......... Unit
Pembahasan:
Misal f(x) keuntungan pada saat memproduksi
dimana keuntungan = pendapatan - biaya produksi
f(x) = (18000x - 80x²) - x.(2000 + 8000/x)
f(x) = -80x² + 18000x - 2000x -8000
f(x) = -80x² + 16000x - 8000
keuntungan akan maksimum jika f'(x) = 0
f'(x) = -160x + 16000 = 0
160x = 16000
x = 16000/160
x = 100
∴ keuntungan maksimum diperoleh pada saat memproduksi komputer sebanyak 100 unit.
Artikel Terkait
- Introductions (Perkenalan)
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?