Keuntungan Mekanis dan Prinsip Kerja Pesawat Sederhana
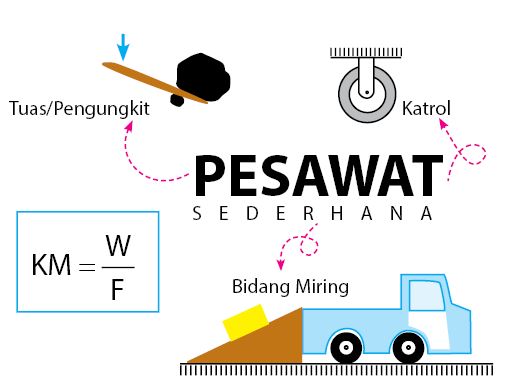
Pesawat sederhana banyak digunakan untuk mempermudah pekerjaan manusia. Hal ini dikarenakan pesawat sederhana memiliki nilai keuntungan mekanis. Ada tiga jenis pesawata sederhana beserta nilai keuntungan mekanis pesawat sederhana yang akan dibahas pada halaman ini. Jenis pesawat sederhana tersebut meliputi tuas atau pengungkit, katrol, dan bidang miring.
Berapa nilai keuntungan mekanis dari masing-masing jenis pesawat sederhana? Simak lanjutan ulasan keuntungan mekanis pesawat sederaha. Meliputi keuntungan mekanis tuas atau pengungkit, keuntungan mekanis katrol, dan keuntungan mekanis bidang miring.
a. Pengungkit/ Tuas
Prinsip Kerja Pengungkit
Ketika akan menggerakan suatu benda dengan memanfaatkan tuas, maka kita harus menempatkan benda di salah satu ujung pengungkit (tuas) kemudian memasang batu atau benda apa saja sebagai titik tumpu dekat dengan benda. Selanjutnya tangan kita memegang ujung batang pengungkit yang nantinya akan diberikan gaya sampai benda bergeser atau dapat diangkat. Berdasarkan posisi titik tumpu, beban, dan kuasanya, pengungkit dibagi menjadi 3 jenis yaitu
Pengungkit Jenis Pertama
Yaitu tuas yang kedudukan titik tumpunya terletak diantara titik beban dan titik kuasa. Peralatan yang prinsip penggunaanya menggunakan pengungkit jenis pertama antara lain pemotong kuku, tang, gunting, linggis, dan jungkat-jungkit.

Keterangan :
A = titik kuasa
T = titik tumpu
B = titik beban
F = gaya kuasa (N)
w = gaya beban (N)
lk = lengan kuasa (m)
lb = lengan beban (m)
Pengungkit Jenis Kedua
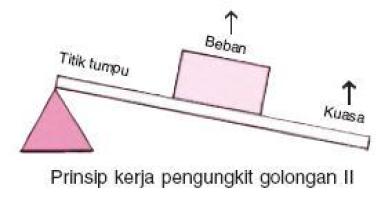
Yaitu tuas yang kedudukan titik bebannya terletak diantara titik tumpu dan titik kuasa. Contoh peralatan yang prinsip penggunaannya menggunakan pengungkit jenis kedua antara lain gerobak beroda satu, alat pemotong kertas, alat pemecah kemiri, dan pembuka tutup botol.
Pengungkit Jenis Ketiga
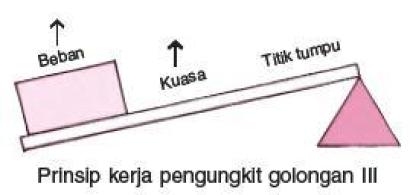
Yaitu tuas yang kedudukan titik kuasanya berada diantara titik beban dan titik tumpu. Contoh peralatan yang prinsip penggunaannya menggunakan pengungkit jenis ketiga antara lain sekop, penjepit roti, stappler, dan pinset.
Keuntungan Mekanis Pengungkit/ Tuas
Pembahasan keuntungan mekanis pesawat sederhana pertama adalah jenis pesawat sederhana yang termasuk dalam tuas atau pengungkit. Tuas dikelompokkan menjadi 3 (tiga), pengelompokan jenis tuas ini didasarkan pada letak kuasa, titik tumpu, dan beban. Tuas jenis pertama memiliki letak titik tumpu yang berada di tengah. Untuk tuas atau pengungkit jenis ke dua memiliki ciri-ciri letak titik beban yang terletak di tengah. Sedangkan tuas dengan titik kuasa yang terletak di tengah dikelompokkan pada kuas jenis ke tiga.
Ada tiga titik yang terdapat pada kuas, yaitu titik tumpu, beban, dan kuasa. Perlu diketahui juga bahwa terdapat istilah lengan beban dan lengan kuasa. Jarak antara titik beban dengan titik tumpu disebut lengan beban. Sedangkan jarak antara titik kuasa dengan titik tumpu disebut lengan kuasa. Keuntungan mekanis tuas diberikan melalui persamaan di bawah.
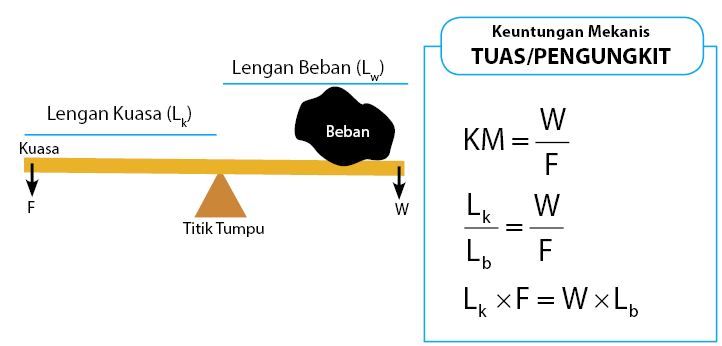
Untuk menambah pemahaman otakers, perhatikan contoh soal keuntungan mekanis tuas/pengungkit beserta dengan pembahasannya berikut ini.
Contoh Soal Keuntungan Mekanis Tuas dan Pembahasan
Sebatang bambu sepanjang 2 meter digunakan sebagai pengungkit untuk memindahkan sebongkah batu seberat 360 N. Pada bambu diletakkan penumpu yang berjarak 20 cm dari batu. Besar kuasa minimal yang harus diberikan pada ujung bambu yang lain agar batu terangkat….
A. 40 N
B. 60 N
C. 80 N
D. 100 N
Pembahasan:
Berdasarkan informasi pada soal, dapat diketahui bahwa:
W (berat batu) = 360 N
L (panjangn kayu) = 2 m
= 20 cm = 0,2 m
Sehingga,
Besar kuasa yang diperlukan untuk mengankat batu adalah
Jawaban: A
b. Keuntungan Mekanis Katrol
Seperti halnya dengan keuntungan mekanis pesawat sederhana jenis tuas, keuntungan mekanis katroldinyatakan melalui perbandingan beban dan kuasa. Perhatikan posisi letak titik tumpu, beban, dan kuasa pada katrol. Nantinya, berdasarkan letak titik tumpu, beban, dan kuasa dapat ditentukan nilai keuntungan mekanis untuk masing-masing jenis katrol.
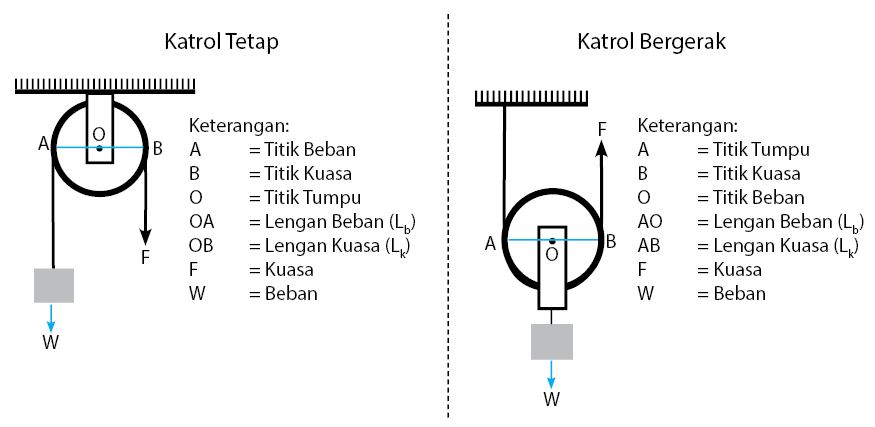
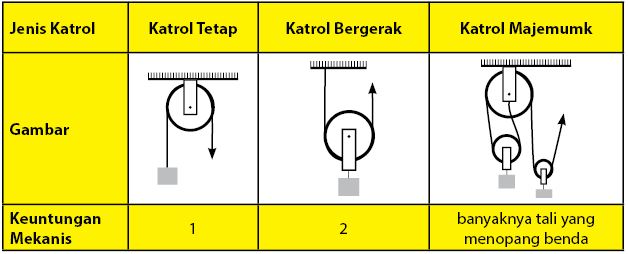
Pada umumnya, ada tiga jenis katrol yang digunakan pada kehidupan sehari-hari, yaitu katrol tetap, katrol bebas, dan katrol bergerak. Dalam katrol, nilai keuntungan mekanis dari tiga jenis katrol tersebut berbeda. Untuk katrol tetap, nilai keuntungan mekanisnya adalah 1 (satu). Pada katrol bergerak, keuntukan mekanis yang dimiliki adalah 2 (dua). Sedangkan pada katrol ganda atau katrol majemuk, keuntungan mekanis katrolnya adalah sejumlah banyak tali yang menopang benda.
Contoh Soal Keuntungan Mekanis Tuas dan Pembahasan
Sebuah benda yang beratnya 200 N diangkat menggunakan katrol bergerak. Gaya yang diperlukan untuk mengangkat beban tersebut adalah ….
A. 50 N
B. 100 N
C. 200 N
D. 400 N
Pembahasan:
Keuntungan mekanis bergerak sama dengan 2, sehingga
Jadi, besar gaya yang dibutuhkan untuk mengangkat beban seberat 200 N adalah 100 N.
c. Keuntungan Mekanis Bidang Miring
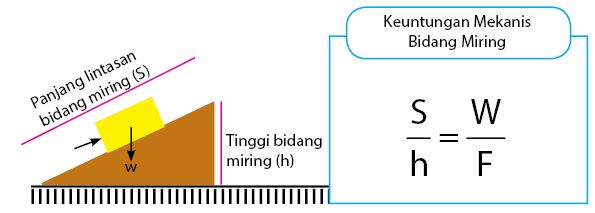
Pembahasan keuntungan mekanis pesawat sederhana berikutnya adalah jenis pesawat sederhana bidang miring. Nilai keuntungan mekanis bidang miring sama juga menggunakan perbandingan berat dan kuasa. Nilain keuntungan mekanis bidang miring akan sebanding dengan nilai perbandingan jarak lintasan bidang miring dan ketinggian bidang miring. Persamaan keuntungan mekanis bidang miring dapat dilihat melalui persamaan di bawah.
Perhatikan pula contoh soal keuntungan mekanis bidang miring berikut untuk menambah pemahaman sobat otakers.
d. Keuntungan Mekanis Roda Berporos
Prinsip penggunaan roda berporos adalah dengan menghubungkan roda pada sebuah poros yang dapat berputar bersama-sama. Manfaat dari roda berporos adalah untuk menggeser suatu benda agar lebih ringan dan memperkecil gaya gesek. Prinsip roda berporos dapat kita jumpai pada alat-alat seperti setir mobil, setir kapal, roda mobil, roda gerobak, dan gerinda
Contoh Soal Keuntungan Mekanis Tuas dan Pembahasan
Perhatikan gambar di bawah!
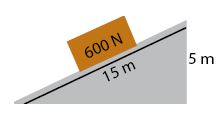
Besar gaya yang dibutuhkan untuk menaikkan barang seberat 600 N menggunkan bidang miring di atas adalah ….
A. 100 N
B. 200 N
C. 600 N
D. 1.200 N
Pembahasan:
Besar gaya yang dibutuhkan untuk menaikkan barang seberat 600 N menggunkan bidang miring tersebut adalah 200 N.
Jawaban: B
Demikianlah ulasan tentang keuntungan mekanis pesawat sederhana. Meliputi keuntungan mekanis tuas, keuntungan mekanis katrol, dan keuntungan mekanis bidang miring. Terimakasih, semoga bermanfaat.
Artikel Terkait
- Setiap Unsur Mampu Membentuk Ikatan Kimia Karena Memiliki...
- Lapisan Tanah Yang Paling Banyak Mengandung Materi Organik Adalah....
- Seekor Burung Terbang dengan Kelajuan 25 m/s. Bila Massa Burung Tersebut Adalah 200 gram. Maka Hitunglah Energi Kinetik yang Dimiliki Burung!
- Kalsium Mempunyai Nomor Atom 20 dan Nomor Massa 40. Jumlah Proton yang Terdapat Dalam Atom Kalsium Adalah ….
- Sinopsis Drama Korea Queen of Tears, Kisah Cinta, Intrik, dan Kejutan yang Mengharukan
- Produk Berikut yang Dibuat Dengan Bantuan Bakteri Adalah ....
- Jumlah Maksimum Elektron Pada Kulit N Adalah ...
- Sifat Fisika yang Dipengaruhi Oleh Perbedaan Massa Atom Partikel Penyusunnya Adalah...
- Sinopsis Drama Korea My Man is Cupid dengan Chemistry Mengagumkan antara Jang Dong-yoon dan Nana
- Rata-rata Ulangan Matematika di Suatu Kelas Adalah 78,4, Sedangkan Simpangan Standarnya 1,5. Jika Andi Adalah Salah Satu Siswa Kelas Tersebut