Sistem Katrol Majemuk
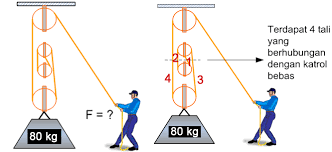
Pembahasan dalam sistem katrol majemuk meliputi persamaan perceptan sistem katrol dan tegangan tali. Sebuah sistem katrol dikategorikan dalam sistem katrol majemuk jika komposisi penyusunnya meliputi katrol tetap dan katrol bebas. Objek atau benda yang terpasang pada sistem katrol dihubungkan oleh tali dan melalui katrol. Contoh sistem katrol majemuk diperlihatkan seperti gambar di bawah.
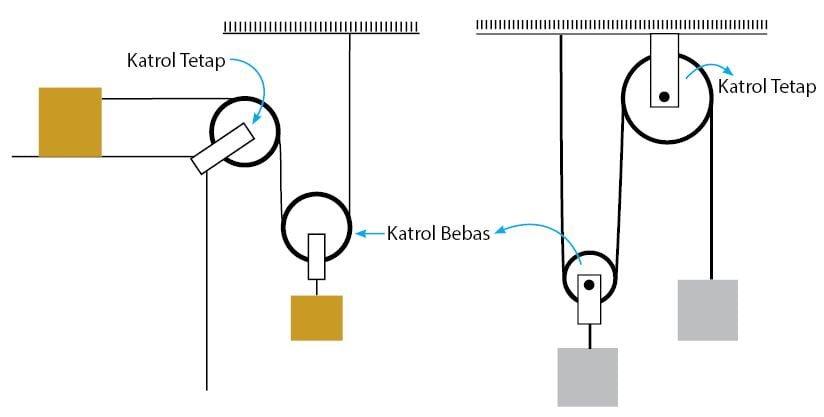
Gambar sebelah kiri, menujukkan sebuah sistem katrol majemuk. Sedangkan gambar di sebelah kanan menunjukkan sebuah sistem katrol majemuk untuk model yang lain. Penyusun kedua sistem katrol di atas adalah sebuah katrol tetap, sebuah katrol bergerak, dan dua buah benda. Perbedaan dari kedua sistem katrol tersebut terletak pada adanya bidang datar pada sistem katrol pertama (sistem katrol sebelah kiri).
Sistem katrol akan mengalami perubahan. Benda akan mengalami pergerakan. Pada sistem katrol mejemuk, terdapat dua percepatan. Kedua percepatan tersebut berlaku untuk percepatan pada benda pertama dan benda ke dua. Berikut ini adalah contoh perubahan sistem katrol dari kondisi awal, setelah selang beberapa waktu.
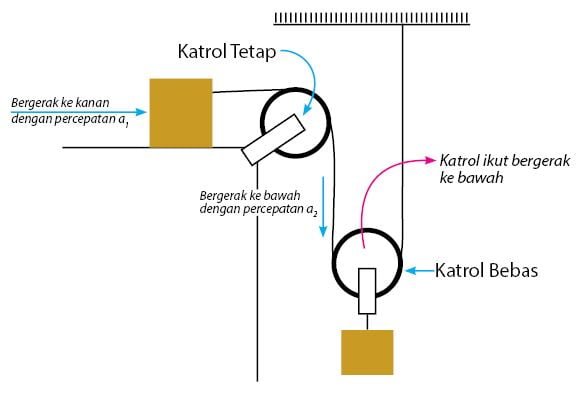
Benda pertama, benda yang terletak pada bidang datar, akan bergerak ke arah kanan dengan percepatan . Benda kedua, benda yang tergantung pada katrol bebas, akan bergerak ke bawah bersama dengan katrol bebasnya.
Pembahasan pada sistem katrol majemuk di sini akan diberikan dalam tiga kelompok. Pertama, pembahasan meliputi sistem katrol majemuk tanpa ada bidang datar. Kedua, pembahasan akan mengulas persamaan pada sebuah sistem katrol majemuk dengan bidang datar licin (mengabaikan gaya gesek). Untuk pembahasan yang ketiga, ulasan yang akan dibahas seperti pada pembahasan pertama dengan meilhat pengaruh gaya gesek pada sistem katrol tersebut.
Simak pembahasan lebih lengkapnya pada uraian di bawah.
Sistem Katrol Majemuk Tanpa Bidang
Sebuah sistem katrol majemuk disusun atas dua buah benda dan dua buah katrol. Dua benda tersebut dihubungkan oleh sebuah tali yang melalui kedua buah katrol. Katrol yang digunakan adalah dua jenis katrol yang berbeda. Kedua jenis katrol tersebut adalah katrol tetap dan katrol bebas. Gambar sistem katrol majemuk ini dapat dilihat seperti gambar di bawah.
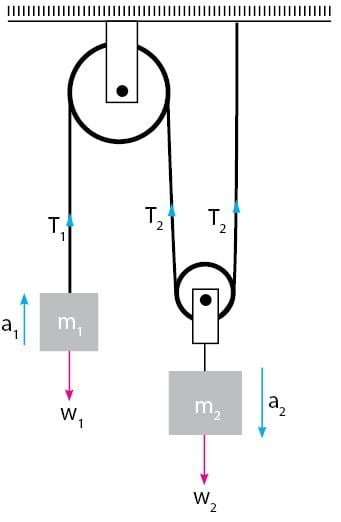
Berdasarkan Hukum Newton dan gaya-gaya yang bekerja pada sistem katrol majemuk di atas akan diperoleh persamaan percepatan sistem katrol majemuk berikut.
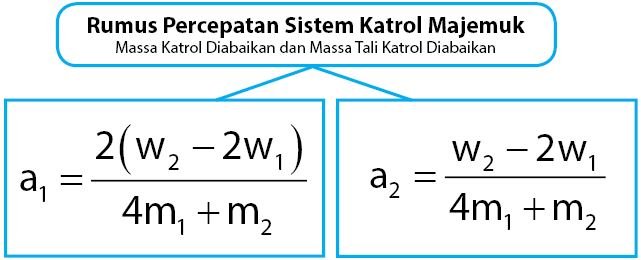
Keterangan:
= percepatan benda pertama
= percepatan benda ke dua
= berat benda ke dua (N)
= berat benda ke dua (N)
= massa benda pertama (kg)
= massa benda ke dua (kg)
Langkah-langkah untuk mendapatkan rumus percepatan sistem katrol majemuk akan diberikan di bawah. Sebelumnya perhatikan kembali detail gaya yang bekerja pada sistem katrol majemuk tanpa bidang di atas.
Tinjau Benda 1:
Tinjau Benda 2:
Karena tegangan tali pada benda pertama sama dengan tegangan tali pada benda ke dua, maka
= w_{2} - m_{2} \cdot a_{2} \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-c4503638c949caf74d667a4c3bfa5f71_l3.svg" style="height:14px; width:211px" title="Rendered by QuickLaTeX.com" />
Demikianlah ulasan sistem katrol majemuk tanpa bidang. Pembahasan selanjutnya merupakan ulasan sistem katrol majemuk dan bidang datar.
Sistem Katrol Majemuk dan Bidang Datar Licin
Diberikan sebuah sistem katrol majemuk, terdiri atas dua buah benda dan dua buah katrol. Sebuah benda terletak pada bidang datar licin. Karena permukaan bidang yang digunakan licin maka gaya gesek diabaikan. Sebuah benda lainnya tergantung pada sebuah katrol bebas. Dua benda tersebut dihubungkan oleh tali dan melalui katrol tetap dan katrol bebas. Gambar sistem katrol mejemuk ini dapat dilihat seperti gambar di bawah.

Pada sistem katrol majemuk di atas, berlaku:
- Tegangan tali sama (
=
= T)
- Bidang datar licin sehingga gaya gesek diabaikan
- Percepatan benda pertama tidak sama dengan percepatan benda ke dua,
= 2
Rumus percepatan sistem katrol majemuk dan bidang datar licin ditunjukkan seperti persamaan di bawah.
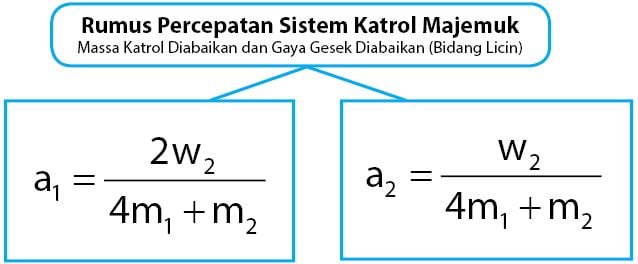
Keterangan:
= percepatan benda pertama
= percepatan benda ke dua
= massa benda ke dua (N)
= massa benda pertama (kg)
= massa benda ke dua (kg)
Dari mana rumus percepatan sistem katrol majemuk tersebut diperoleh? Berikut ini adalah langkah-langkah untuk mendapatkan rumus percepatan sistem katrol majemuk tersebut. Sebelumnya, perhatikan kembali detail gaya yang diberikan pada sistem katrol majemuk di atas.
Tinjau Benda 1:
Tinjau Benda 2:
Tegangan tali pada benda pertama sama dengan tegangan tali pada benda ke dua, sehingga
Selanjutnya, akan dilihat pengaruh gaya gesek pada sistem katrol majemuk dan bidang datar.
Sistem Katrol Majemuk dan Bidang Datar Kasar
Permasalahan pada sistem katrol ini sama dengan sebelumnya. Hanya saja, bidang datar yang digunakan di sini memiliki permukaan yang kasar, sehingga terdapat gaya gesek. Kita akan melihay pengaruh gaya gesek tersebut terhadap persamaan yang telah didapatkan sebelumnya. Berikut ini adalah detai gaya yang bekerja pada sistem katrol majemuk dan bidang datar kasar.
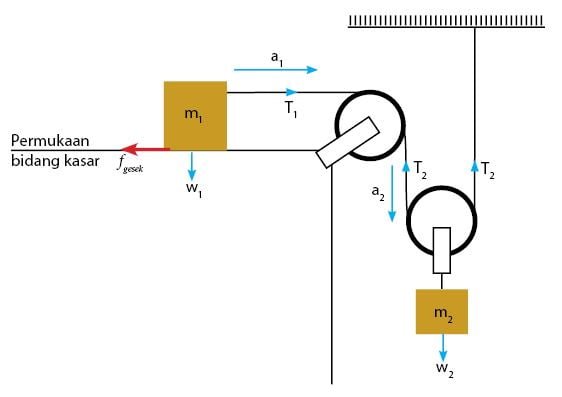
Ketentuan yang berlaku untuk sistem katrol majemuk dan bidang datar kasar adalah sebegai berikut.
- Tegangan tali sama
=
= T
- Permukaan bidang datar yang digunakan kasar, sehingga terdapat gaya gesek
- Percepatan benda tidak sama
Bagaimana pengaruh gaya gesek pada sistem katrol majemuk ini?
Rumus percepatan sistem katrol mejemuk dan bidang datar kasar diberikan seperti persamaan di bawah.
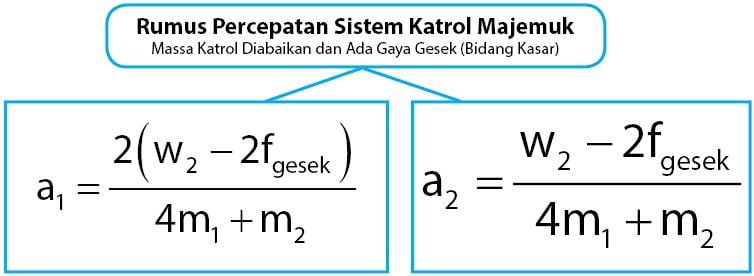
Keterangan:
= percepatan benda pertama
= percepatan benda ke dua
= gaya gesek (N)
= berat benda ke dua (N)
= massa benda pertama (kg)
= massa benda ke dua (kg)
Langha-langkah mendapat rumus percepatan sistem katrol majemuk dengan memperhatikan gaya geseknya adalah sebagai berikut.
Tinjau Benda 1:
Tinjau Benda 2:
Karena tegangan tali pada benda pertama sama dengan tegangan tali pada benda ke dua, maka
= w_{2} - m_{2} \cdot a_{2}\]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-c5b8dda948658749a42a8f714ada50d6_l3.svg" style="height:15px; width:208px" title="Rendered by QuickLaTeX.com" />
Kesimpulannya, gaya gesek akan membuat percepatan sistem katrol majemuk menjadi lebih kecil.
Untuk menambah pemahaman sobat idschool akan diberikan contoh penggunaan uraian rumus percepatan sistem katrol di atas. Simak contoh soal sistem katrol majemuk dan pembahasannya berikut ini.
CONTOH SOAL DAN PEMBAHASAN
Sebuah sistem katrol majemuk dirangkai seperti pada gambar di bawah.
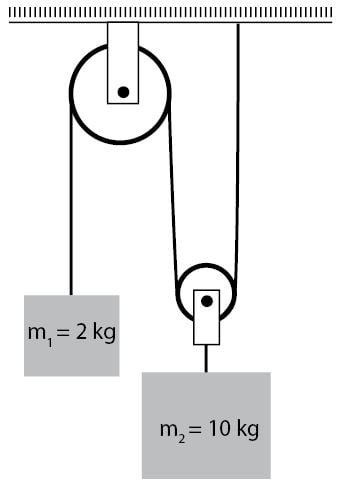
Dua buah balok, pertama dan ke dua berturut-turut memiliki massa 2 kg dan 10 kg. Percepatan gravitasi bumi diketahu sebesar 10 . Jika katrol licin serta massa tali dan katrol diabaikan, maka tentukanlah percepatan masing-masing balok adalah ….
Pembahasan:
Detail uraian gaya yang bekerja pada sistem katrol tersebut dapat dilihat seperti gambar di bawah.
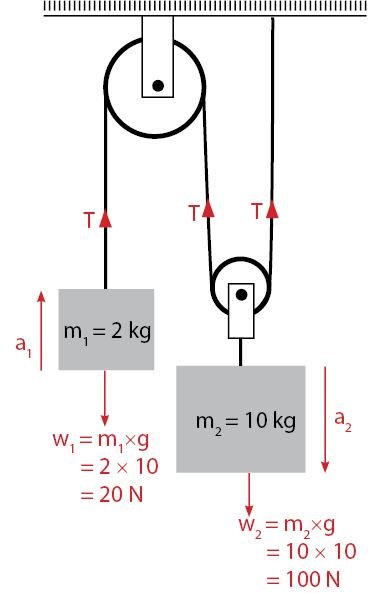
Untuk mendapatkan nilai percepatan pada sistem katrol tersebut, sobat idschool hanya perlu menggunakan rumus percepatan yang telah diulas pada pembahasan di atas. Pilih rumus percepatan sistem katrol yang sesuai dengan kondisi pada soal yang diberikan. Seperti berikut ini.
Mencari percepatan pada benda pertama ():
Mencari percepatan pada benda ke dua ():
Jadi, percepatan masing-masing balok adalah = 6,67
dan
= 3,33
.
Jawaban: A
Demikianlah tadi ulasan tentang sistem katrol majemuk. Meliputi 3 (tiga) rumus percepatan sistem katrol majemuk untuk tiga kondisi yang berbeda. Terimakasih, semoga bermanfaat.
Artikel Terkait
- Hujan dan air mengalir dapat mengikis tanah tanah yang paling banyak terkikis oleh hujan dan air mengalir adalah tanah dari
- 5 Drama Korea Terbaik yang Diperankan oleh Song Kang, Pilihan Menarik untuk Ditonton Selama Wajib Militer
- Berikut Ini yang Bukan Merupakan Partikel Penyusun Atom Adalah...
- Berikut Ini yang Bukan Merupakan Sifat Fisika Suatu Zat Adalah
- Drama Korea Queen of Tears Menjadi Sensasi dengan Rating Tinggi, Apa yang Menanti di Episode Selanjutnya?
- Setiap Unsur Mampu Membentuk Ikatan Kimia Karena Memiliki...
- Lapisan Tanah Yang Paling Banyak Mengandung Materi Organik Adalah....
- Seekor Burung Terbang dengan Kelajuan 25 m/s. Bila Massa Burung Tersebut Adalah 200 gram. Maka Hitunglah Energi Kinetik yang Dimiliki Burung!
- Kalsium Mempunyai Nomor Atom 20 dan Nomor Massa 40. Jumlah Proton yang Terdapat Dalam Atom Kalsium Adalah ….
- Sinopsis Drama Korea Queen of Tears, Kisah Cinta, Intrik, dan Kejutan yang Mengharukan