Persamaan Nilai Mutlak Linier Satu Variabel Beserta Contoh Soal

Nilai mutlak merupakan sebuah nilai yang selalu bernilai positif serta biasa dinotasikan seperti | x |. Di dalam bidang ilmu geometri, nilai mutlak merupakan sebuah jarak dari x ke 0 pada garis bilangan real. Sebab jarak tersebut selalu bernilai positif atau nol, sehingga nilai mutlak x juga akan selalu bernilai positif atau nol untuk masing-masing setiap x bilangan real.
Secara umum, nilai mutlak ini bisa kita jabarkan menjadi sebagai berikut:
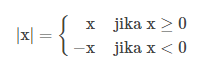
atau dapat pula ditulis
| x | = -x jika x ≥ 0
| x | = -x jika x < 0
Definisi diatas dapat kita maknai sebagai berikut : Nilai mutlak bilangan positif atau nol adalah bilangan itu sendiri dan nilai mutlak bilangan negatif adalah lawan dari bilangan tersebut.
Selain dari persamaan di atas, jika nilai mutlak ada dalam sebuah bentuk aljabar maka bisa kita peroeh sebuah persamaan seperti berikut ini:
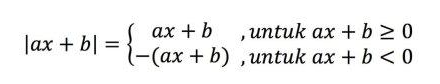
Contoh:
| 5 | = 5
| -4 | = -(-4) = 4
| 3 | + | - 2 | = 3 + 2 = 5
Jadi, jelas bahwa nilai mutlak setiap bilangan real akan selalu bernilai positif atau nol.
Sifat Persamaan Nilai Mutlak
Nilai mutlak dari sebuah bilangan x bisa juga didefiniskan sebagai jarak bilangan tersebut pada titik 0 pada garis bilangan, dengan tidak memperhatikan arahnya.
| x | = a dengan a > 0

Jarak -a ke 0 sama dengan jarak a ke 0, yaitu a. Pertanyaannya adalah dimana x agar jaraknya ke 0 juga sama dengan a.
Posisi x ditunjukkan oleh titik merah pada gambar diatas, yaitu x = -a atau x = a. Jelas terlihat bahwa jarak dari titik tersebut ke 0 sama dengan a. Jadi, agar jarak x ke nol sama dengan a, haruslah x = -a atau x = a.
Contoh soal
1. | 2y + 5 | = | 7 - 2y |
Jawab:
Berdasarkan dari sifat a, maka:
| 2y + 5 | = | 7 - 2y |
⇔ (2y + 5)2 = (7 - 2y)2
⇔ 4y2 + 20y + 25 = 49 - 28y + 4y2
⇔ 48y = 24
⇔ y = 1/2
Sehingga, himpunan penyelesaian adalah HP = {1/2}.
2. Tentukanlah suatu himpunan dari: |3x – 1| = |x + 4|
Jawab:
Berdasarkan dari sifat a, maka:
|3x – 1| = |x + 4|
⇔ 3x – 1 = x + 4 atau 3x – 1 = -(x + 4)
⇔ x = 5 atau 4x = -4
⇔ x = 5 atau x = -1
Sehingga, himpunan penyelesaian dari soal 2 adalah HP = {-1, 5}.